Topic: Pythagorean theorem.
Basic concepts:
Pythagoras was a Greek philosopher and mathematician.
A right triangle is one that has an angle of ninety degrees (90°). In front of it is the hypotenuse, which is the longest. Then we have the opposite leg, it is in front of the hypotenuse and it is the height. Finally, the adjacent leg is at the bottom, which means it is the height.
______________________
We have:
- Hypotenuse: 10 cm
- Opposite leg: 6 cm
- Adjacent leg: ???
Which means that we are going to find the value of one of its legs. We know:
The leg of a right triangle is the square root of the hypotenuse squared, minus the other leg raised to the 2.
We have that its formula is:
![\: \: \: \: \: \: \: \: \: \: \: \: \: \: \boxed{\textbf{c}^{\textbf{2}} = \sqrt[]{\textbf{h}^{\textbf{2}} - \textbf{c}^{\textbf{2 }} } }](https://img.qammunity.org/2023/formulas/spanish/college/fp1bl3rgn5y4lcypw9n1nomp4b5y35jmh2.png)
We solve:
Taking into account the aforementioned formula, we replace by the known values:
![\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: {\boxed{ \sf{c^(2)=\sqrt[]{10^(2) -6^(2) } }}}](https://img.qammunity.org/2023/formulas/spanish/college/y10jh31itmfqh5ox6re448lq94uwh7wewh.png)
We solve what is inside the radicación. That is, we first perform the powers.
![\: \: \: \: \: \: \: \: \: \: \: \: \: \: \boxed{ \sf \: c^(2) = \sqrt[]{100 - 36} }](https://img.qammunity.org/2023/formulas/spanish/college/yu1eelq50k4w87p7njlkxhz65bygyh1hfu.png)
We do the remainder:
![\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \boxed{ \sf \: c^(2) = \sqrt[]{64} }](https://img.qammunity.org/2023/formulas/spanish/college/e5b5896qs2jmdobm024za4wtrszcmk4ifj.png)
The exponent 2 will go to the root, this means that we have to take the square root of 64.
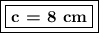
Answer: The value of the missing (adjacent) leg is 8 cm.