Answer:
Approximately
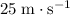 (assuming that air resistance on the marble is negligible, and that
(assuming that air resistance on the marble is negligible, and that
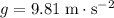 .)
.)
Step-by-step explanation:
Start by finding the duration
 of the flight of the marble.
of the flight of the marble.
If the air resistance on the marble is negligible, the marble will accelerate downward at a constant
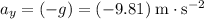 .
.
Let
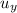 denote the initial vertical velocity of the marble. Let
denote the initial vertical velocity of the marble. Let
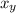 denote the vertical displacement (change in height) of the marble.
denote the vertical displacement (change in height) of the marble.
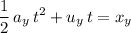 .
.
Since the marble was launched horizontally,
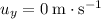 . This equation becomes:
. This equation becomes:
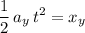 .
.
The marble was launched from a height of
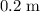 above the floor. When the marble lands, it would be
above the floor. When the marble lands, it would be
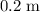 below where it was launched. Hence, the vertical displacement of the flight will be
below where it was launched. Hence, the vertical displacement of the flight will be
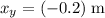 .
.
Solve the equation for
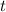 :
:
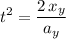 .
.
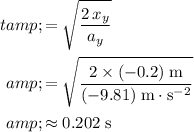 .
.
In other words, the marble was in the air for approximately
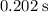 before landing.
before landing.
Also because the air resistance on the marble is negligible, the horizontal velocity of the marble will be constant during the entire flight.
The marble achieved a horizontal displacement
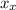 of
of
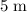 in that flight of approximately
in that flight of approximately
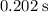 . Hence, the (initial) horizontal velocity
. Hence, the (initial) horizontal velocity
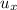 of the marble will be:
of the marble will be:
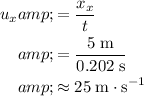 .
.
Combine both the initial horizontal and vertical velocity of the marble to find the initial speed
 :
:
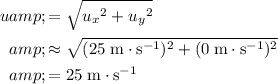 .
.