Answer:
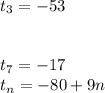
Explanation:
Arithmetic sequence:

Here a is the first term and d is the common difference.
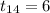 ⇒
⇒
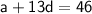 ------------(I)
------------(I)
 ⇒ a + 19d = 100 ---------(II)
⇒ a + 19d = 100 ---------(II)
Subtract equation (I) from (II)
(I1) a + 19d = 100
(II) a + 13d = 46
- - -
6d = 54
d = 54 ÷ 6
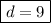
Substitute d = 9 in equation(I) and find 'a',
a + 13*9= 46
a + 117 = 46
a = 46 - 117
a = -71
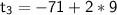
= -71 + 18
= -53
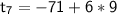
= -71 + 54
= -17
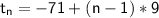
= -71 + 9*n - 1 *9
= -71 + 9n - 9
= -71 - 9 + 9n
= - 80 + 9n