Answer:
a) a = 13
b) see explanation
c) x = 10
d) b = 13
Explanation:
a) Use the Pythagorean Theorem as directed by the problem.
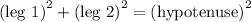
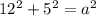
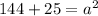
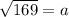
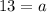
a = 13
b) △ABE and △ACD:
- share angle C, and all right angles are congruent.
- share angle A, and any angle is congruent to itself.
- Therefore, they are similar using the AA theorem.
c) To solve for x, compare the ratios of the bottom sides to the right sides.
12 : (12 + 12)
12 : 24 → 24 = 12 · 2
5 : x
x = 5 · 2
x = 10
d) Since we have already found the other two sides of △ACD, we can find its hypotenuse using the Pythagorean theorem and some extra algebra.
LET

--------------------------------



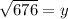

Now that we have solved for y, we can now plug y into the auxiliary equation from the beginning of step d.


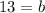
b = 13