Question

Consider a circle with center C(5,8) that contains the point P(1,2) What is the radius? What is the circle equation?

Answer 1

see explanation

Explanation:

the radius r is the distance from the centre to a point on the circle.

calculate the radius using the distance formula

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2 }`

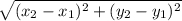
with (x₁, y₁ ) = P (1, 2 ) and (x₂, y₂ ) = C (5, 8 )

r =
`√((5-1)^2+(8-2)^2)`

=
`√(4^2+6^2)`

=
`√(16+36)`

=
`√(52)`

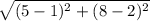
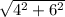
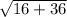
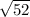
the equation of a circle in standard form is

(x - h )² + (y - k )² = r²

where (h, k ) are the coordinates of the centre and r is the radius

here (h, k ) = C (5, 8 ) and r =
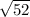`√(52)` , then

(x - 5 )² + (y - 8 )² = (
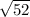`√(52)` )² , that is

(x - 5)² + (y - 8)² = 52