Question

A van has a weight of 4000 lb and center of gravity at Gv. It carries a fixed 900 lb load which has a center of gravity at Gl. If the van is traveling at 40 ft/s, determine the distance it skids before stopping. The brakes cause all the wheels to lock or skid. The coefficient of kinetic friction between the wheels and the pavement is . Assume that the two rear wheels are one normal, NB, and the two front wheels are one normal, NA.

Answer 1

x = 25 / μ [ ft]

Step-by-step explanation:

To solve this exercise we can use Newton's second law.

Let's set a reference system where the x axis is parallel to the road

Y axis

N_B + N_A - W_van - W_load = 0

N_B + N_A = W_van + W_load

X axis

fr = ma

a = fr / m

the total mass is

m = (W_van + W_load) / g

the friction force has the expression

fr = μ N_{total}

fr = μy (W_van + W_load)

we substitute

a = μ (W_van + W_load)
`(g)/(W_van + W_load)`

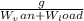
a = μ g

taking the acceleration let's use the kinematic relations where the final velocity is zero

v² = v₀² - 2 a x

0 = v₀² -2a x

x =
`(v_o^2)/(2a)`

x =
`(v_o^2)/(2 \mu g)`

x =
`(40^2)/(2 \ 32 \ \mu)`

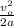
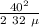
x = 25 / μ [ ft]