Question

Calculus Ladder Sliding Down

Answer 1

`\left.\frac{\text{d}x}{\text{d}t}\right|_(h=2)\approx0.184\; \sf m/s`

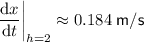
Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

Given variables:

• a = length of the ladder.
• h = height of the ladder's top at time t.
• x = distance of the ladder from the wall at time t.

Given a = 8.9, use Pythagoras Theorem to create an equation for x² in terms of h²:

`\implies x^2+h^2=a^2`

`\implies x^2+h^2=8.9^2`

`\implies x^2+h^2=79.21`

`\implies x^2=79.21-h^2`

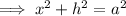
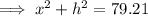
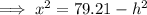
Differentiate with respect to h:

`\implies 2x\frac{\text{d}x}{\text{d}h}=0-2h`

`\implies \frac{\text{d}x}{\text{d}h}=-(2h)/(2x)`

`\implies \frac{\text{d}x}{\text{d}h}=-(h)/(x)`

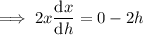
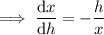
Given:

`\frac{\text{d}h}{\text{d}t}=-0.8\; \sf m/s`

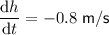
Therefore:

`\begin{aligned} \frac{\text{d}x}{\text{d}t}&=\frac{\text{d}x}{\text{d}h}* \frac{\text{d}h}{\text{d}t}}\\\\ \implies &=-(h)/(x) * -0.8\\\\ &=(0.8h)/(x) \end{aligned}`

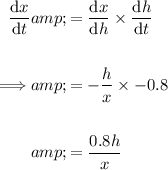
Calculate x when h = 2:

`\implies x^2=79.21-2^2`

`\implies x^2=79.21-4`

`\implies x^2=75.21`

`\implies x=√(75.21)`

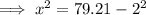
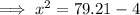
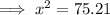
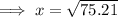
Substitute the values of h and x into the equation for dx/dt:

`\implies \frac{\text{d}x}{\text{d}t}=(0.8 * 2)/(√(75.21))=0.1844939751`

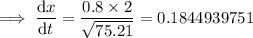
Therefore, the rate of the ladder's distance from the wall is 0.184 m/s (3 d.p.)