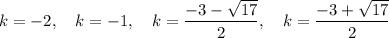Answer:
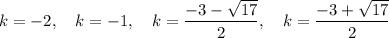
Explanation:
Given equation of the parabola:
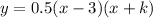
x-intercepts
The x-intercepts are the points at which the curve crosses the x-axis.
To find the x-intercepts, substitute y = 0 into the given equation and solve for x:
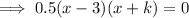
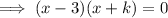
Apply the zero-product property:
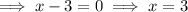
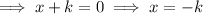
Therefore, the x-intercepts are:
y-intercept
The y-intercept is the point at which the curve crosses the y-axis.
To find the y-intercept, substitute x = 0 into the given equation and solve for y:
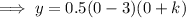
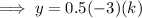
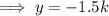
Therefore, the y-intercept is:
Area

The height of the triangle is the distance between the y-intercept and the x-axis:
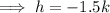
The base of the triangle is the difference between the x-intercepts:
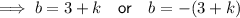
Given the area of the triangle is equal to 1.5 square units, substitute the values of b and h into the formula for area and solve for k:
For b = (3 + k):
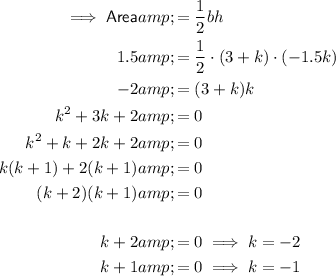
For b = -(3 + k):
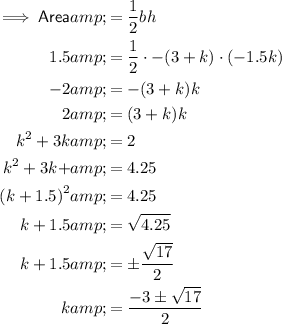
Solution
Therefore, the possible values of k are: