Answer:
Approximately
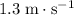 .
.
Step-by-step explanation:
When an ideal spring with spring constant
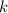 is displaced by
is displaced by
 from equilibrium, the elastic potential energy (
from equilibrium, the elastic potential energy (
 ) stored in the spring will be:
) stored in the spring will be:
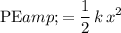 .
.
If an object of mass
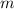 is travelling at a speed of
is travelling at a speed of
 , the kinetic energy (
, the kinetic energy (
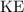 ) of that object will be:
) of that object will be:
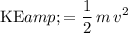 .
.
Under the assumptions of this question, all the elastic potential energy (
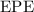 ) stored in the spring would have been turned into the kinetic energy (
) stored in the spring would have been turned into the kinetic energy (
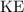 ) of the disk.
) of the disk.
Let
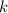 and
and
 denote the spring constant and displacement from equilibrium of this spring. Let
denote the spring constant and displacement from equilibrium of this spring. Let
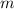 and
and
 denote the mass and speed of the disk. Apply unit conversion and ensure that the displacement of the spring is in standard units (meters):
denote the mass and speed of the disk. Apply unit conversion and ensure that the displacement of the spring is in standard units (meters):
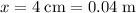 .
.
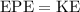 .
.
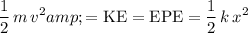 .
.
Rearrange this equation to find the speed of the disk
 :
:
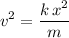 .
.
Since speed
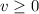 :
:
 .
.
(Note that
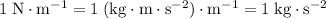 .)
.)
Hence, the speed of the disk would be approximately
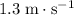 .
.