Answer:

Explanation:
The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:
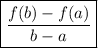
The given interval is 30 ≤ x ≤ 60.
Therefore:
From inspection of the table:
- f(a) = f(30) = 13
- f(b) = f(60) = 19
Substitute the values into the formula:
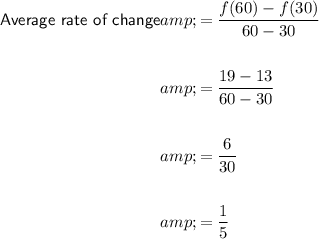
Therefore the average rate of change in simplest form of the given function over the interval 30 ≤ x ≤ 60 is ¹/₅.