Question

A certain drug has a half-life in the body of 3.5h. Suppose a patient takes one 200.Mg pill at :500PM and another identical pill 90min later. Calculate the amount of drug left in his body at :700PM.

Answer 1

The amount of drug left in his body at 7:00 pm is 315.7 mg.

Step-by-step explanation:

First, we need to find the amount of drug in the body at 90 min by using the exponential decay equation:

`N_(t) = N_(0)e^(-\lambda t)`

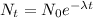
Where:

λ: is the decay constant =
`ln(2)/t_(1/2)`

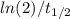
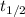`t_(1/2)`: is the half-life of the drug = 3.5 h

N(t): is the quantity of the drug at time t

N₀: is the initial quantity

After 90 min and before he takes the other 200 mg pill, we have:

`N_(t) = 200e^{-(ln(2))/(3.5 h)*90 min*(1 h)/(60 min)} = 148.6 mg`

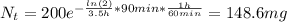
Now, at 7:00 pm we have:

`t = 7:00 pm - (5:00 pm + 90 min) = 30 min`

`N_(t) = (200 + 148.6)e^{-(ln(2))/(3.5 h)*30 min*(1 h)/(60 min)} = 315.7 mg`

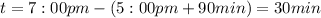
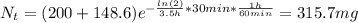
Therefore, the amount of drug left in his body at 7:00 pm is 315.7 mg (from an initial amount of 400 mg).

I hope it helps you!