Question

Determine whether each statement is always, sometimes, or never true.

13. For a 0, the value of a¹ is positive. ●

14. If n is an integer, then 3" 3" equals 1.

15. If 6P 0, then p > 0. 16. 4* equals 1. 4*

17. If m is an integer, then the value of 2m is negative​

Answer 1

Problem 13

Answer: Sometimes true

Reason:

If a > 0, then the statement would always be true. However, if 'a' was negative, then the statement is false.

For example, if a = -2 then:

`a^(-1) = (-2)^(-1) = (1)/((-2)^1) = -(1)/(2) = -0.5`

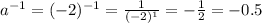
In short,

`a^(-1) = -0.5 \ \ \text{ when } a = -2`

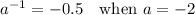
This is one of infinitely many counter-examples to prove the original statement isn't always true.

===================================================

Problem 14

Answer: Always true

Reason:

The rule to use here is
`a^b*a^c = a^(b+c)`

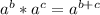
We add exponents b and c, while the base 'a' stays the same the whole time.

In this problem we have:
`3^n*3^(-n) = 3^(n+(-n)) = 3^(n-n) = 3^0 = 1`

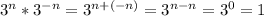
Therefore
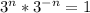`3^n*3^(-n) = 1` is always true regardless of what you replace n with. The variable n doesn't have to be an integer.

===================================================

Problem 15

Answer: Sometimes true

Reason:

Let's say p = -1 is plugged into the expression

`6^p = 6^(-1) = (1)/(6^1) = (1)/(6) \approx 0.1667`

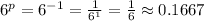
which is a positive outcome showing that
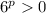`6^p > 0` doesn't automatically guarantee that p > 0. Feel free to try other negative values as counter-examples. Also p = 0 works as well. It turns out that
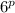`6^p` is always positive regardless of what real number you use for p.

===================================================

Problem 16

Answer: Always true

Reason:

The rule used here is
`a^(-b) = (1)/(a^b)`

An equivalent rule is
`\left((a)/(b)\right)^(-c) = \left((b)/(a)\right)^c`

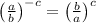
The idea is to flip the fraction to turn the exponent positive.

Examples:
`2^(-5) = (1)/(2^5) \ \ \text{ and } \ \ \left((7)/(9)\right)^(-3) = \left((9)/(7)\right)^(3)`

===================================================

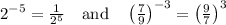
Problem 17

Answer: Never true

Reason:

This is similar to problem 15 in that
`2^m` is always positive regardless if m is negative, zero, or positive. It might help to graph out
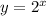`y = 2^x` and see that the curve never dips below the x axis.