Answer:
1) Slope = -11, y-intercept = 6
2) Slope = 3/2, y-intercept = -4/3
3) Slope = 2/3, y-intercept = -5/6
4) Slope = -5, y-intercept = 13
5) Slope = 5/2, y-intercept = -8
Explanation:

To find the slope and y-intercept of each equation, rearrange each equation so that it is in slope-intercept form.
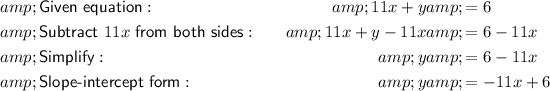
Therefore:
- Slope = -11
- y-intercept = 6
--------------------------------------------------------------------------------------------
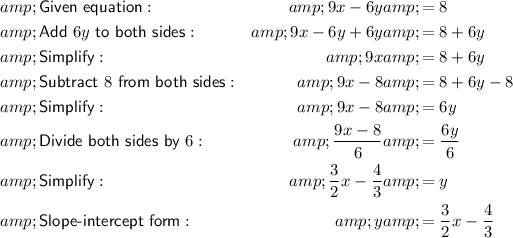
Therefore:
- Slope = 3/2
- y-intercept = -4/3
--------------------------------------------------------------------------------------------

Therefore:
- Slope = 2/3
- y-intercept = -5/6
--------------------------------------------------------------------------------------------

Therefore:
- Slope = -5
- y-intercept = 13
--------------------------------------------------------------------------------------------
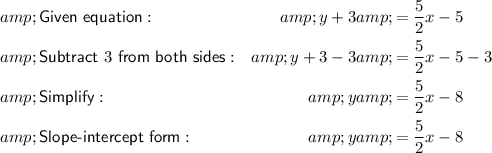
Therefore:
- Slope = 5/2
- y-intercept = -8