Question

Write and solve a system of equations that represents the scenario below. Be sure to define your variables, and

answer the question.


Ricky Bobby and Betty Sue are super hungry after doing all of these problems, so they ask their uncle Billy Joe Bob to
take them to "Burgers and Dogs" for some tasty mini burgers and mini hot dogs. Ricky Bobby orders 3 mini burgers
and 2 mini dogs for $8. Betty Sue orders 2 mini dogs and 1 mini burger for $6. How much would Uncle Billy Joe Bob spend if he ordered 3 mini dogs and 4 mini burgers?
Can someone help me!

Answer 1

Answer: $11.50

==================================================

Step-by-step explanation:

x = cost of one burger

y = cost of one hot dog

3 burgers = 3x dollars

2 hot dogs = 2y dollars

3 burgers + 2 hot dogs = 3x+2y = 8 dollars

The first equation to set up is 3x+2y = 8 which is based on the info of what Ricky purchased.

Through similar logic, the other equation is x+2y = 6 based on what Betty ordered.

This is the system of equations

`\begin{cases}3x+2y = 8\\x+2y = 6\end{cases}`

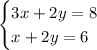
There are a few approaches we could take. I'll use substitution.

Let's isolate x in the 2nd equation.

x+2y = 6

x = -2y+6

Then plug this into the 1st equation. Solve for x.

3x + 2y = 8

3(-2y+6) + 2y = 8

-6y+18+2y = 8

-4y+18 = 8

-4y = 8-18

-4y = -10

y = -10/(-4)

y = 2.50 dollars is the cost of one hot dog

Then,

x = -2y+6

x = -2*2.50+6

x = -5+6

x = 1 dollar is the cost of one burger

-----------------------

Check:

• Ricky: 3x+2y = 3*1+2*2.50 = 3 + 5 = 8 dollars spent
• Betty: x+2y = 1+2*2.50 = 1+5 = 6 dollars spent

The x and y values are confirmed correct.

------------------------

The last thing to find out is how much is spent if Billy bought 4 burgers and 3 hot dogs

4x+3y = 4*1 + 3*2.50 = 4 + 7.50 = 11.50 dollars is the final answer

This assumes that Billy is paying for himself and the other people pay for themselves as well. If Billy is paying for everyone, then the total comes to 11.50+8+6 = 25.50 dollars.