Answer:
14 inches
Explanation:
The side lengths of an equilateral triangle are the congruent.
The side lengths of a square are the congruent.
Let x be the length of one side of the equilateral triangle.
⇒ Perimeter of triangle = 3x
Let y be the length of one side of the square.
⇒ Perimeter square = 4y
Given:
- The perimeter of the triangle is 10 inches more than the perimeter of the square.
- The side of the triangle is 6 inches longer than the side of the square.
Create a system of equations with the given information and defined variables:
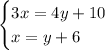
Substitute the second equation into the first equation and solve for y:
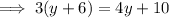
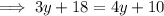
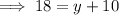
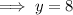
Therefore, the side length of the square is 8 inches.
Substitute the found value of y into the second equation and solve for x:
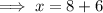
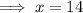
Therefore, the side length of the triangle is 14 inches.