Answer:
Approximately
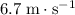 at approximately
at approximately
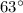 west from north (
west from north (
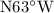 .)
.)
Step-by-step explanation:
The velocity of both vehicles can be described with a two-dimensional vector:
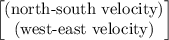 .
.
(Note that the two directions are perpendicular to one another.)
For example, since the cookie vehicle is travelling north at
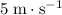 , its velocity vector will be:
, its velocity vector will be:
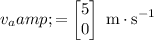 .
.
Likewise, the velocity vector of the milk vehicle travelling west at
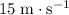 will be:
will be:
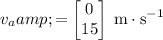 .
.
When an object of mass
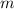 travels at a velocity of
travels at a velocity of
 , the momentum
, the momentum
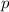 of that object will be
of that object will be
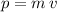 .
.
The momentum vector of the
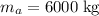 cookie vehicle will be:
cookie vehicle will be:
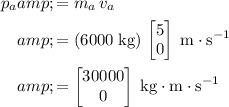 .
.
The momentum vector of the
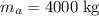 milk vehicle will be:
milk vehicle will be:
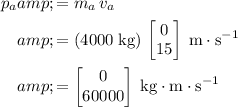 .
.
Hence, the total momentum of the two vehicles before the collision will be:
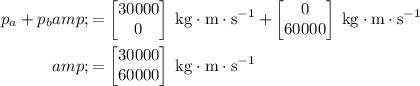 .
.
Let
 denote the velocity vector of the two vehicles right after they collide. With a total mass of
denote the velocity vector of the two vehicles right after they collide. With a total mass of
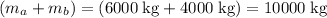 , the total momentum of the two vehicles right after the collision will be:
, the total momentum of the two vehicles right after the collision will be:
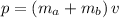 .
.
Momentum is conserved. Hence, right after collision, the total momentum of the two vehicles will stay the same. Thus,
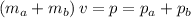 .
.
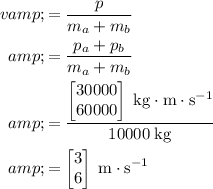 .
.
Since the two directions (north-south and west-east) are perpendicular to each other, the Pythagorean Theorem can be applied to find the magnitude of this velocity:
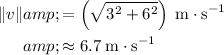 .
.
The angle between this velocity and the direction of north can be found as:
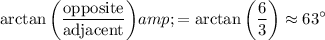 .
.