
Given :-
- The area of rectangular trampoline is 135ft².
- The length of the trampoline is 6ft greater than the width of the trampoline .
To Find :-
- We have to find the width of the trampoline
Let's Begin :-
We have,
- Area of rectangular trampoline = 135ft²
Let the width of the rectangular trampoline be w
According to the question,
- Length is 6ft greater than width
Therefore,
The length of the rectangular trampoline will be
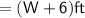
Now,
We know that,

Subsitute the required values,
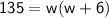
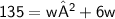
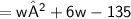
By factorization method,
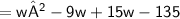
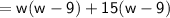

Therefore,
Width of the rectangular trampoline
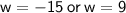
[ Width of the rectangle can never be negative ]
Thus , The width of the rectangular trampoline is 9 feet
