We are looking for the value of t when d(t) equals 250. So:
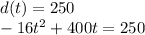
So let's solve for t. The best way to do this is by using the Quadratic Formula. This evaluates quadratic equations. Quadratic equations are trinomials with a degree of two.
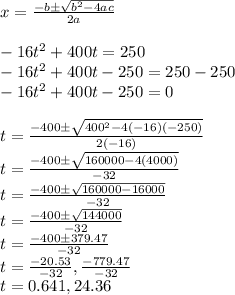
So the projectile will be at a height of 250ft at 0.641 seconds and 24.36 seconds.