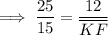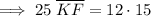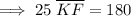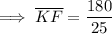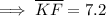Answer:
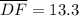
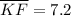
Explanation:
Vertical Angles Theorem
When two straight lines intersect, the opposite vertical angles are congruent.
Alternate Interior Angles Theorem
If a line intersects a set of parallel lines in the same plane at two distinct points, the alternate interior angles that are formed are congruent.
Given DE is parallel to KL.
According to the vertical angles theorem:
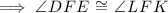
Therefore, according to the alternate interior angles theorem:
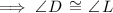
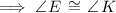
As all three angles of triangle DEF are congruent to the corresponding angles in triangle LKF, the triangles are similar.
In similar triangles, corresponding sides are always in the same ratio.
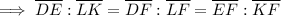
Given:
- DE = 25
- LK = 15
- LF = 8
- EF = 12
Therefore:
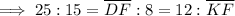
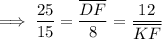
Solving for DF:

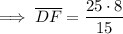
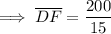

Solving for KF: