Answer:
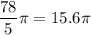
Explanation:
Given values:
- Radius (r) = 5.2
- Arc length = 6π
As the arc length is given in terms of pi, use the formulas where the angle is measured in radians.

Substitute the given values into the arc length formula to calculate the central angle (in radians):
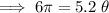
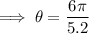
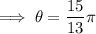

Substitute the radius and the found angle into the formula and solve for area:
