Question

The radius of a regular hexagon is 8 cm.

Find the apothem, perimeter and area
of the regular hexagon.

Answer 1

the measure of the side = of the measure of radius because the regular hexagon have 6 sides = at each others

meaning the measure the perimeter is = 6 times the radius

and the radius = 8cm

so perimeter = 6× 8 cm

perimeter = 48cm

since the apothem is the segment perpendicular to a side thought the center and those segment are not promotional we have the notation as

r square root of 3 divided by 2

r = radius = 8 cm

by apply the formula

8square root 3 divided by 2

so the area will be

since the perimeter is 48cm

and the apothem is 8 square root of 3 divided 2

so the area will be 48 times 8 square root of 3 divided by 2 = 384 square of 3 divided by 2 .

hope that helps.

Answer 2

The apothem of the hexagon is 8 cm, the perimeter is 48 cm, and the area is approximately 96√3
`cm^2`.

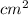How to find the apothem, perimeter, and area of a regular hexagon

To find the apothem, perimeter, and area of a regular hexagon with a given radius, use the following formulas:

Apothem (a):

The apothem of a regular hexagon is the distance from the center of the hexagon to the midpoint of any side (flat side).

In a regular hexagon, the apothem is equal to the radius.

Thus, in this case, the apothem is 8 cm.

Perimeter (P):

The perimeter of a regular hexagon is the sum of the lengths of all its sides. Since a regular hexagon has six equal sides, calculate the perimeter by multiplying the length of one side by 6.

The length of one side can be found using the formula:

Side length = 2 * radius * sin(π/6)

In this case, the radius is 8 cm, so the side length would be:

Side length = 2 * 8 cm * sin(π/6) ≈ 2 * 8 cm * 0.5 = 8 cm

Therefore, the perimeter would be:

P = 6 * side length = 6 * 8 cm = 48 cm

Area (A):

The area of a regular hexagon can be found using the formula:

Area = (3 * √3 * side lengt
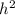`h^2`) / 2

Using the side length of 8 cm, calculate the area as follows:

Area = (3 * √3 * 8
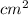`cm^2`) / 2 ≈ 3 * √3 * 64
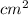`cm^2` / 2 = 96√3
`cm^2`

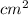
Therefore, the apothem of the hexagon is 8 cm, the perimeter is 48 cm, and the area is approximately 96√3
`cm^2`.