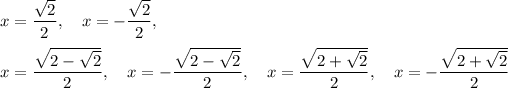Question

Solve the equation without using a calculator


`x^2+\big(4x^3-3x\big)^2=1`

Answer 1

`x= (√(2))/(2), \quad x=-(√(2))/(2),\\\\x=\frac{\sqrt{2 - √(2)}}{2}, \quad x=-\frac{\sqrt{2 - √(2)}}{2}, \quad x= \frac{\sqrt{2 + √(2)}}{2}, \quad x= -\frac{\sqrt{2 + √(2)}}{2}`

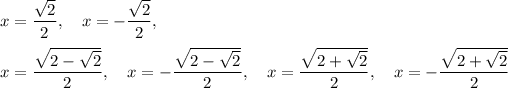
Explanation:

Given equation:

`x^2+(4x^3-3x)^2=1`

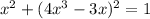
Expand and equal the equation to zero:

`\begin{aligned}x^2+(4x^3-3x)^2&=1\\x^2+(4x^3-3x)(4x^3-3x)&=1\\x^2+16x^6-24x^4+9x^2&=1\\16x^6-24x^4+x^2+9x^2-1&=0\\16x^6-24x^4+10x^2-1&=0\end{aligned}`

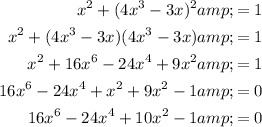
Let u = x²:

`\implies 16u^3-24u^2+10u-1=0`

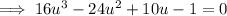
Factor Theorem

If f(x) is a polynomial, and f(a) = 0, then (x – a) is a factor of f(x)

`\textsf{As\;\;$f\left((1)/(2)\right)=0$\;\;then\;$\left(u-(1)/(2)\right)$\;is a factor of $f(u)$}.`

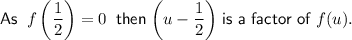
Therefore:

`\implies \left(u-(1)/(2)\right)\left(16u^2+bu+2\right)=0`

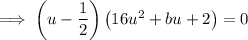
Compare the coefficients of u² to find b:

`\implies b-8 = -24`

`\implies b = -16`

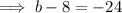
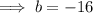
Therefore:

`\implies \left(u-(1)/(2)\right)\left(16u^2-16u+2\right)=0`

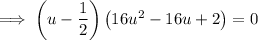
Factor out 2:

`\implies 2\left(u-(1)/(2)\right)\left(8u^2-8u+1\right)=0`

`\implies \left(u-(1)/(2)\right)\left(8u^2-8u+1\right)=0`

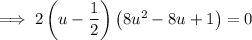
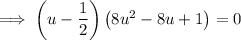
Zero Product Property

If a ⋅ b = 0 then either a = 0 or b = 0 (or both).

Using the Zero Product Property, set each factor equal to zero and solve for u.

`\implies u-(1)/(2)=0 \implies u=(1)/(2)`

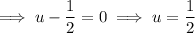
Use the quadratic formula to solve the quadratic:

`\implies u=(-(-8) \pm √((-8)^2-4(8)(1)))/(2(8))`

`\implies u=(8 \pm √(32))/(16)`

`\implies u=(8 \pm 4√(2))/(16)`

`\implies u=(2 \pm √(2))/(4)`

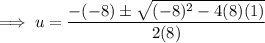
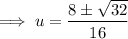
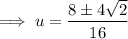
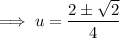
Therefore:

`u=(1)/(2), \quad u=(2 - √(2))/(4), \quad u=(2 + √(2))/(4)`

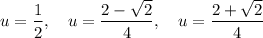
Substitute back u = x²:

`x^2=(1)/(2), \quad x^2=(2 - √(2))/(4), \quad x^2=(2 + √(2))/(4)`

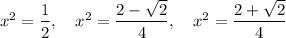
Solve each case for x:

`\implies x^2=(1)/(2)`

`\implies x=\pm \sqrt{(1)/(2)}`

`\implies x=\pm (√(2))/(2)`

`\implies x^2=(2 - √(2))/(4)`

`\implies x=\pm \sqrt{(2 - √(2))/(4)}`

`\implies x=\pm \frac{\sqrt{2 - √(2)}}{2}`

`\implies x^2=(2 + √(2))/(4)`

`\implies x=\pm \sqrt{(2 + √(2))/(4)}`

`\implies x=\pm \frac{\sqrt{2 + √(2)}}{2}`

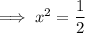
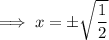
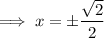
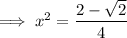
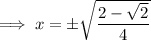
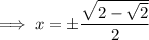
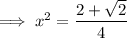
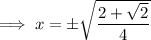
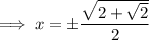
Solutions

`x= (√(2))/(2), \quad x=-(√(2))/(2),\\\\x=\frac{\sqrt{2 - √(2)}}{2}, \quad x=-\frac{\sqrt{2 - √(2)}}{2}, \quad x= \frac{\sqrt{2 + √(2)}}{2}, \quad x= -\frac{\sqrt{2 + √(2)}}{2}`