Answer:
A. K = 59.5
Step-by-step explanation:
Hello there!
In this case, since this reaction seems to start moving leftwards due to the fact that neither A nor Y are present at equilibrium, we should rewrite the equation:
3C (g) + D (g) <-- --> 2A (g) + Y (g)
Thus, the equilibrium expression is:
![K^(left)=([A]^2[Y])/([C]^3[D])](https://img.qammunity.org/qa-images/2022/formulas/chemistry/college/zxbrqdoghbyblzpj7usbhq.png)
Next, according to an ICE table for this reaction, we find that:
![[A]=2x](https://img.qammunity.org/qa-images/2022/formulas/chemistry/college/u3gpu2k30wntoqcddd581o.png)
![[Y]=x](https://img.qammunity.org/qa-images/2022/formulas/chemistry/college/ay5u63hbdvs8dt8xxdtyon.png)
![[C]=0.651M-3x](https://img.qammunity.org/qa-images/2022/formulas/chemistry/college/nh3j6irdfvta6s4jaemkw4.png)
![[D]=0.754M-x](https://img.qammunity.org/qa-images/2022/formulas/chemistry/college/qsxnn5chfs8ng7p8b6497x.png)
Whereas x is calculated by knowing that the [C] at equilibrium is 0.456M; thus:
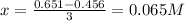
Next, we compute the rest of the concentrations:
![[A]=2(0.065M)=0.13M](https://img.qammunity.org/qa-images/2022/formulas/chemistry/college/bgijsjdob0hrz1zh8ltysn.png)
![[Y]=0.065M](https://img.qammunity.org/qa-images/2022/formulas/chemistry/college/ikxwbpb9w1xlrje09o16p7.png)
![[D]=0.754M-0.065M=0.689M](https://img.qammunity.org/qa-images/2022/formulas/chemistry/college/j1dkkskbbgq9j6hm072uzo.png)
Thus, the equilibrium constant for the leftwards reaction is:
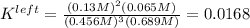
Nonetheless, we need the equilibrium reaction for the rightwards reaction; thus, we take the inverse to get:
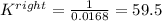
Therefore, the answer would be A. K = 59.5.
Regards!