Question

2A (g) + Y (g) <-- --> 3C (g) + D (g)

Based on the initial conditions shown below, determine the value of the equilibrium constant if the concentration of product C at equilibrium was measured to be 0.456 M.
Initial Conditions: No reactants present, [C] = 0.651 M, [D] = 0.754 M.
Equilibrium Conditions: [A] = ?, [Y] = ?, [C] = 0.456 M, [D] = ?.

A. K = 59.5
B. K = 37.2
C. K = 0.0269
D. K = 0.0168

Answer 1

A. K = 59.5

Step-by-step explanation:

Hello there!

In this case, since this reaction seems to start moving leftwards due to the fact that neither A nor Y are present at equilibrium, we should rewrite the equation:

3C (g) + D (g) <-- --> 2A (g) + Y (g)

Thus, the equilibrium expression is:

`K^(left)=([A]^2[Y])/([C]^3[D])`

Next, according to an ICE table for this reaction, we find that:

`[A]=2x`

`[Y]=x`

`[C]=0.651M-3x`

`[D]=0.754M-x`

Whereas x is calculated by knowing that the [C] at equilibrium is 0.456M; thus:

`x=(0.651-0.456)/(3) =0.065M`

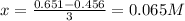
Next, we compute the rest of the concentrations:

`[A]=2(0.065M)=0.13M`

`[Y]=0.065M`

`[D]=0.754M-0.065M=0.689M`

Thus, the equilibrium constant for the leftwards reaction is:

`K^(left)=((0.13M)^2(0.065M))/((0.456M)^3(0.689M))=0.0168`

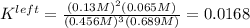
Nonetheless, we need the equilibrium reaction for the rightwards reaction; thus, we take the inverse to get:

`K^(right)=(1)/(0.0168)=59.5`

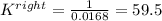
Therefore, the answer would be A. K = 59.5.

Regards!