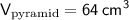Question

A pyramid has a square base of length 8cm and a total surface area of 144cm². Find the volume of the pyramid. (Please use Pythagoras' Theorem thank you)

Answer 1

`\displaystyle V_{ \text{pyramid}}= 64 \: {cm}^(3)`

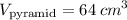
Explanation:

we are given surface area and the length of the square base

we want to figure out the Volume

to do so

we need to figure out slant length first

recall the formula of surface area

`\displaystyle A_{\text{surface}}=B+(1)/(2)* P * s`

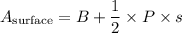
where B stands for Base area

and P for Base Parimeter

so

`\sf\displaystyle \: 144=(8 * 8)+(1)/(2)* (8 * 4) * s`

now we need our algebraic skills to figure out s

simplify parentheses:

`\sf\displaystyle \: 64+(1)/(2)*32* s = 144`

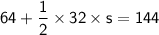
reduce fraction:

`\sf\displaystyle \: 64+\frac{1}{ \cancel{ \: 2}}* \cancel{32} \: ^(16) * s = 144 \\ 64 + 16 * s = 144`

simplify multiplication:

`\displaystyle \: 16s + 64 = 144`

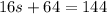
cancel 64 from both sides;

`\displaystyle \: 16s = 80`

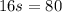
divide both sides by 16:

`\displaystyle \: \therefore \: s = 5`

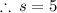
now we'll use Pythagoras theorem to figure out height

according to the theorem

`\displaystyle \: {h}^(2) + ((l)/(2) {)}^(2) = {s}^(2)`

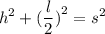
substitute the value of l and s:

`\displaystyle \: {h}^(2) + ((8)/(2) {)}^(2) = {5}^(2)`

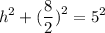
simplify parentheses:

`\displaystyle \: {h}^(2) + (4 {)}^(2) = {5}^(2)`

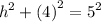
simplify squares:

`\displaystyle \: {h}^(2) + 16 = 25`

cancel 16 from both sides:

`\displaystyle \: {h}^(2) = 9`

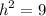
square root both sides:

`\displaystyle \: \therefore \: {h}^{} = 3`

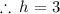
recall the formula of a square pyramid

`\displaystyle V_(pyramid)=(1)/(3)* A* h`

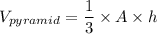
where A stands for Base area (l²)

substitute the value of h and l:

`\sf\displaystyle V_{ \text{pyramid}}=(1)/(3)* \{8 * 8 \}* 3`

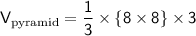
simplify multiplication:

`\sf\displaystyle V_{ \text{pyramid}}=(1)/(3)* 64* 3`

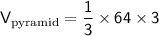
reduce fraction:

`\sf\displaystyle V_{ \text{pyramid}}=\frac{1}{ \cancel{ 3 \: }}* 64* \cancel{ \: 3}`

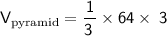
hence,

`\sf\displaystyle V_{ \text{pyramid}}= 64 \: {cm}^(3)`