Question

an electron is trapped in a one-dimensional region of width 0.062 nm. find the three smallest possible values allowed for the energy of the electron.

Answer 1

`1.6 * 10^(-17) J, 6.3 * 10^(-17) J, 1.4 * 10^(-16) J`

Step-by-step explanation:

The equation for the energy of a particle in a 1d "box" (line) is
`(n^2h^2)/(8mL^2)`

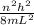
n equals any positive integer, and h is a constant. m is the mass of the electron, and l is the length of the box.

when n = 1, plug in 6.626*10^-34 for h, 9.1093837 *10^-31 for m, and 6.2*10^-11 m for L

(6.626*10^-34)^2 / (8* 9.1093837*10^-31 * (6.2*10^-11)^2 ) which equals
1.56725802e-17 joules
when n = 2, the energy is greater than when n = 1 by a factor of 2^2, or 4. so, the energy it has when n = 2 is

1.56725802e-17 * 4, or 6.26903208e-17 joules

when n = 3, the energy equals

3^3 * 1.56725802e-17, or 9 * 1.56725802e-17, or 1.41053222e-16 joules

round to 2 sig figs to get

1.6 * 10^-17 J, 6.3 * 10^-17 J, and 1.4 * 10^-16 J