Question

PLS HELP QUICK. Determine which integer will make the inequality 12 > 2x + 4 true.

S:{8}
S:{4}
S:{12}
S:{−2}

Answer 1

The number that makes the inequality true is D, -2

Explanation:

• Reverse the inequality

`2x+4 < 12`

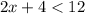
• Subtract by the lone number to the left; 4

`2x+4-4 < 12-4\\2x+4-4\\=2x+\left(4-4\right)\\= 4-4\\= 2x+0\\=2x`

-------------

`12-4\\= 8`

`= 2x < 8`

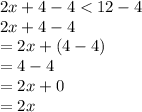
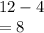
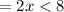
• Divide by the leading coefficient; 2. Assume x = 1

`(2x)/(2) < (8)/(2)`

`(2x)/(2) = (2* x)/(2) = (2)/(2) = x`

-------------------------

`(8)/(2) = 4`

• Thus,

`\bold{x < 4}`

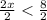
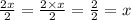
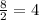
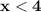
• Because x is less than 4, the only number less than 4 is -2. Therefore, D is your answer.

Hope this helps!

Answer 2

S:{-2}

Explanation:

12 > 2(-2) + 4

12 > -4 + 4

12 > 0