Answer:
see explanation
Explanation:
given that W varies jointly with l and d² then the equation relating them is
W = kld² ← k is the constant of variation
(a)
to find k use the condition W = 6 when l = 6 and d = 3 , then
6 = k × 6 × 3² = 6k × 9 = 54k ( divide both sides by 54 )
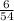= k , then
k =
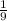
W =
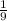ld² ← equation of variation
(b)
when W = 10 and d = 2 , then
10 =
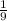× l × 2² ( multiply both sides by 9 to clear the fraction )
90 = 4l ( divide both sides by 4 )
22.5 = l
(c)
when d = 6 and l = 1.4 , then
W =
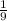× 1.4 × 6² =
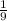× 1.4 × 36 = 1.4 × 4 = 5.6