Answer:
18 candy bars sold.
5 bag of chips sold.
Explanation:
To determine the number of candy bars sold and the number of bags of chips sold, we can set up and solve a system of equations.
Define the variables:
- Let x be the number of candy bars sold.
- Let y be the number of bags of chips sold.
Given the price of each candy bar is $1.50, the price of each bag of chips is $1.25, and the total Melanie made was $33.25:
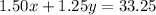
Given Melanie sold 13 more candy bars than bags of chips:

Therefore, the system of equations is:
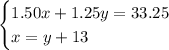
To solve the system of equations, substitute the second equation into the first equation to eliminate x:
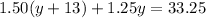
Solve for y:
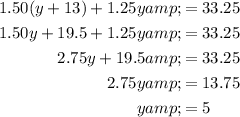
Therefore, Melanie sold 5 bags of chips.
To find the number of candy bars sold, we can substitute the found value of y = 5 into the second equation and solve for x:
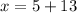
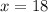
Therefore, Melanie sold 18 candy bars.