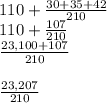Question

Express the integral as a limit of Riemann sums using right endpoints. Do not evaluate the limit.

Answer 1

23,207/210

Explanation:

`\int\limits^7_4 {x^(2)+(1)/(x) } \, dx \\`

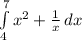
Right endpoints start at 7

It doesn't say how many so I will assume there are 3.

7, 6, 5

Plug in those values into the integrand:

7^2+ 1/7=

49+1/7

6^2+1/6=

36+1/6

5^2+1/5=

25+1/5

1(49+1/7+36+1/6+25+1/5)

110+1/7+1/6+1/5 The least common factor of 7,6,5 is 210

`110 + (30+35+42)/(210) \\110 + (107)/(210) \\(23,100+107)/(210) \\\\(23,207)/(210) \\`