Answer:
- smaller x value: -1,-8
- larger x value: 5,16
The parenthesis part is already taken care of by the teacher.
=================================================
Step-by-step explanation:
y is equal to x^2-9 and also 4x-4. We can equate those two right hand sides and get everything to one side like this
x^2-9 = 4x-4
x^2-9-4x+4 = 0
x^2-4x-5 = 0
Then we can use the quadratic formula to solve that equation for x.
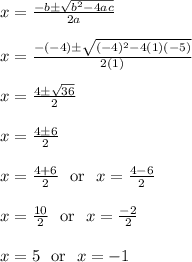
Or alternatively
x^2-4x-5 = 0
(x-5)(x+1) = 0
x-5 = 0 or x+1 = 0
x = 5 or x = -1
------------------------------
After determining the x values, plug them into either original equation to find the paired y value.
Let's plug x = 5 into the first equation:
y = x^2-9
y = 5^2-9
y = 25-9
y = 16
Or you could pick the second equation:
y = 4x-4
y = 4(5)-4
y = 20-4
y = 16
We have x = 5 lead to y = 16
One solution is (x,y) = (5,16)
This is one point where the two curves y = x^2-9 and y = 4x-4 intersect.
If you repeat the same steps with x = -1, then you should find that y = -8 for either equation.
The other solution is (x,y) = (-1,-8)