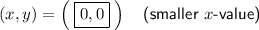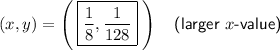Answer:
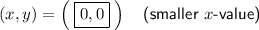
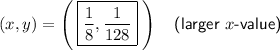
Explanation:
Given system of equations:
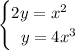
To solve by the method of substitution, substitute the second equation into the first equation, rearrange so that the equation equals zero, then factor:
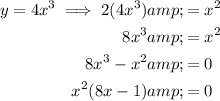
Apply the zero-product property to solve for x:
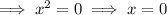
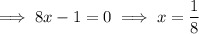
Substitute the found values of x into the second equation and solve for y:
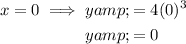
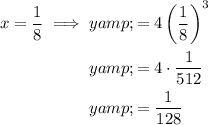
Therefore, the solutions are: