In point form, (1, 1, 0), or equation form:
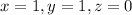
_________________________________________________
How So?
Well,....
Isolate x for -2x + 2y + 3z = 0:
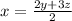
Substitute
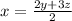 :
:
![[-2*(2y+3z)/(2)-y+z=-3; 2*(2y+3z)/(2)+3y+3z=5]](https://img.qammunity.org/2023/formulas/mathematics/college/ucfqsaf2i8czqqt24ye4syqpy3q86lunay.png)
Simplify:
![[-3y-2z=-3; 5y+6z=5]](https://img.qammunity.org/2023/formulas/mathematics/college/6duamw93e8zf4udsdy7mdrv1vrx7jj0syd.png)
Isolate y for -3y - 2z = -3:
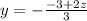
Substitute y = - -3+2z/3:
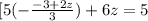
Simplify:
![[(15+8z)/(3)=5]](https://img.qammunity.org/2023/formulas/mathematics/college/8wwqv666cbesrx7tl8bdau2kmyfe3p5mnn.png)
Isolate z for [15+8z/3 = 5]:
For y = - -3+2z/3
Substitute z = 0
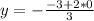
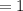
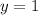
For x = 2y+3z/2
Substitute z = 0, y = 1
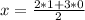
Simplify:

Hence, the solutions to the system of equations are:
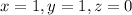
Hope this helps!