Answer:
Approximately
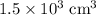 (approximately
(approximately
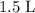 .)
.)
Step-by-step explanation:
Look up the density of mercury:
 .
.
The density of water is
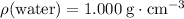 .
.
Multiply the horizontal cross-section area
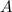 by height
by height
 to find the volume of mercury in this cylinder:
to find the volume of mercury in this cylinder:
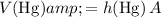 .
.
The mass of that much mercury will be:
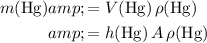 .
.
The mass of the liquid is proportional to the pressure that the liquid exerts on the bottom of the cylinder.
In this question, the pressure of the added water need to match that of the mercury in the container, so that the total pressure will double. Hence, the mass of the added water will need to be equal to that of the mercury in the cylinder.
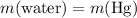 .
.
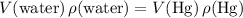 .
.
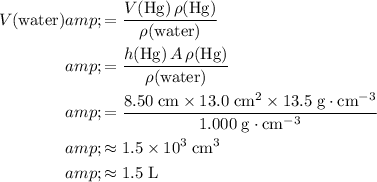 .
.