Question

The total surface area of a cone of slant height 1cm and base radius rcm is 224πcm,if r:1=2:5 find

a. correct to one decimal place,the value of r
b. correct to the nearest whole number, the value of the cone. (take π 22/7​

Answer 1

a. r = 8 cm

b. The volume of the cone is approximately 1,229 cm³

Explanation:

The given parameters are;

The slant height of the cone = l cm

The base radius of the cone = r cm

The total surface area of the cone = 224·π cm

r : l = 2 : 5

Therefore, we have;

`(r)/(l) = (2)/(5)`

`r= (2)/(5) * l`

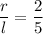
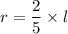
The total surface area of a cone, T.S.A. = π·r·l + π·r²

The total surface area of the cone, T.S.A. cone = π × (2/5)·l² + π·((2/5)·l)²

T.S.A. cone = π × (2/5)·l² + π·((2/5)·l)² = π·((2/5)·l² + (4/25)·l²)

T.S.A. cone = π·l²·((2/5) + (4/25)) = (14/25)·π·l²

∴ T.S.A. cone = 224·π cm² = (14/25)·π·l²

l² = 224 cm² × 25/14 = 400 cm²

l = √(400 cm²) = 20 cm

`r= (2)/(5) * l = (2)/(5) * 20 \, cm = 8 \, cm`

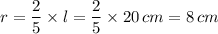
r = 8 cm

b. The volume of a cone, V = 1/3·π·r²·h

Where;

h = The height of the cone

By Pythagoras's theorem, h = √(l² - r²)

∴ h = √(20² - 8²) = √(336) = 4·√(21)

The height of the cone, h = 4·√(21)

The volume of the cone, V = 1/3 × (22/7) × 8² × 4·√(21) ≈ 1,229.00315781

∴ The volume of the cone, V to the nearest whole number ≈ 1,229 cm³.