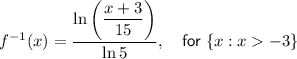Question

Find the inverse of
`f(x)=3*5^x^+^1-3` and give the domain in interval form of the resulting function.

Answer 1

`f^(-1)(x)=( \ln \left( (x+3)/(15) \right) )/( \ln 5), \quad \textsf{for}\; \{x : x > -3 \}`

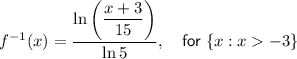
Explanation:

Given function:

`f(x)=3 \cdot 5^(x+1)-3`

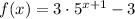
The domain of the given function is unrestricted: (-∞, +∞).

The range of the given function is restricted: (-3, +∞).

The inverse of a function is its reflection in the line y = x.

To find the inverse of a function, replace x with y:

`\implies x=3 \cdot 5^(y+1)-3`

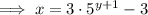
Rearrange the equation to make y the subject:

`\implies x=3 \cdot 5^(y+1)-3`

`\implies x=3 \cdot 5^y \cdot 5^1-3`

`\implies x=15 \cdot 5^y -3`

`\implies x+3=15 \cdot 5^y`

`\implies (x+3)/(15)= 5^y`

`\implies \ln \left( (x+3)/(15) \right) = \ln 5^y`

`\implies \ln \left( (x+3)/(15) \right) = y \ln 5`

`\implies y=( \ln \left( (x+3)/(15) \right) )/( \ln 5)`

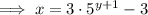
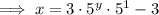
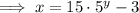
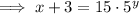
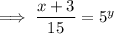
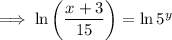
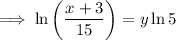
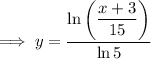
Replace y with f⁻¹(x):

`\implies f^(-1)(x)=( \ln \left( (x+3)/(15) \right) )/( \ln 5)`

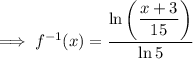
The domain of the inverse of a function is the same as the range of the original function.

Therefore, the domain of the inverse function is (-3, +∞).

Therefore, the inverse of the given function is:

`f^(-1)(x)=( \ln \left( (x+3)/(15) \right) )/( \ln 5), \quad \textsf{for}\; \{x : x > -3 \}`