Question

Please help solving these questions! I’ve literally worked this for 40 mins

Answer 1

slope: -1/2
X intercepts: (6, 0)
Y intercepts: (0,3)
Equation: y=( -1/2)x + 3
Slope of the line perpendicular to the line: 2

Answer 2

1) (6, 0), (0, 3)

2) -½

3) y= -½x +3

4) -½

5) 2

Explanation:

1) x- intercept is the point at which the line passes though the x-axis.

From the graph, the x- intercept is (6, 0).

The y-intercept is the point at which the line passes through the y- axis.

From the graph, the y-intercept is (0, 3).

2) To find the slope, plug in the coordinates of any two points on the line into the gradient formula below.

`\boxed{slope = (y1 - y2)/(x1 - x2) }`

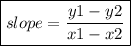
I will use the 2 points that they have provided to calculate the slope.

`slope = (5 - ( - 2))/( - 4 - 10)`

`slope = (7)/( - 14)`

`slope = - (1)/(2)`

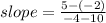
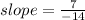
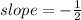
3) The equation of a line can be written as y= mx +c, where m is the gradient and c is the y-intercept.

Since we have already found those values in the previous questions, let's substitute them into the equation.

`y = - (1 )/(2) x + 3`

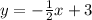
4) Parallel lines have the same slope.

Thus, the slope of a line parallel to the line in the graph will also have a slope of -½.

5) The product of the gradients of perpendicular lines is -1.

(gradient of perpendicular line)(-½)= -1

Gradient of perpendicular line

`= - 1 / - (1)/(2)`

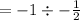
= 2