Question

In the diagram, what is the relationship between segments AC and BC? Explain your answer.

Answer 1

`\overline{AC} \cong \overline{BC}`

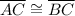
"line segment AC is congruent to line segment BC"

Explanation:

First, establish that the two triangles
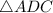`\triangle ADC` and
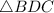`\triangle BDC` are congruent.

The triangles share side
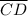`\overline{CD}`, and through the reflexive property of congruence, we know that any line segment is congruent to itself.

Angles
`\angle ADC` and
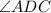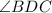`\angle BDC` are congruent because they are supplementary, and
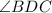`\angle BDC` is a right angle, or its measure is 90°; therefore the other angle must also be 90°, and angles with the same measure are congruent.

It is given that
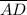`\overline{AD}` and
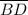`\overline{BD}` are congruent.

Now, it can be proven that
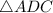`\triangle ADC` and
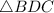`\triangle BDC` are congruent using the SAS theorem.

Finally,
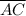`\overline{AC}` is congruent to
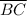`\overline{BC}`, or
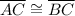`\overline{AC} \cong \overline{BC}`, because of the Corresponding Parts of Congruent Triangles are Congruent theorem (CPCTC).