Answer:
![[d(A, B)]^2=\boxed{85}](https://img.qammunity.org/2023/formulas/mathematics/college/r1h30u8vdi5gqfbiiwb1k4ht3fs6b6p3hx.png)
![[d(A,C)]^2+[d(B,C)]^2=\boxed{85}](https://img.qammunity.org/2023/formulas/mathematics/college/4rs9dnp2izucji9ait9x7cbuyeiiqq4go0.png)
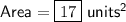
Explanation:
From inspection of the given diagram, the vertices of the triangle are:
- A = (-5, 5)
- B = (1, -2)
- C = (-1, 6)
If ΔABC is a right triangle, the sum of the squares of the two shorter sides will equal the square of the longest side. This is the definition of Pythagoras Theorem.
Use the distance formula to find the side lengths of the triangle.

![\begin{aligned}d[(A,B)]&=√((x_B-x_A)^2+(y_B-y_A)^2)\\&=√((1-(-5))^2+(-2-5)^2)\\&=√((6)^2+(-7)^2)\\&=√(36+49)\\&=√(85)\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/lgh4t4kkli9jg30bbfkmtnvdsfeej0vy4q.png)
![\begin{aligned}d[(A, C)]&=√((x_C-x_A)^2+(y_C-y_A)^2)\\&=√((-1-(-5))^2+(6-5)^2)\\&=√((-4)^2+(1)^2)\\&=√(16+1)\\&=√(17)\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/6q7mswduay8o6yw056ub8tcdue241uzmer.png)
![\begin{aligned}d[(B, C)]&=√((x_C-x_B)^2+(y_C-y_B)^2)\\&=√((-1-1)^2+(6-(-2))^2)\\&=√((-2)^2+(8)^2)\\&=√(4+64)\\&=√(68)\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/hh0v16g4r6eowonqdyq4ujgu6wldcdosch.png)
Therefore:
- The longest side of the triangle is line segment AB.
- The two shorter sides of the triangle are line segments AC and BC.

The triangle is a right triangle if:
![[d(A,C)]^2+[d(B,C)]^2=[d(A,B)]^2](https://img.qammunity.org/2023/formulas/mathematics/college/xlzqtg7r57p7cqlf08bpu7tr32th6m72pq.png)
Substitute the found side lengths into the formula:
![\implies [√(17)]^2+[√(68)]^2=[√(85)]^2](https://img.qammunity.org/2023/formulas/mathematics/college/1mx3ei4jenjazgwzwp3jlyw41fdsln9tny.png)
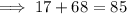
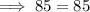
Therefore, this proves that ΔABC is a right triangle.
To find the area of a right triangle, half the product of the two shorter sides:
![\begin{aligned}\implies \sf Area &= (1)/(2)bh\\&=(1)/(2) \cdot [d(A,C)] \cdot [d(B,C)]\\&=(1)/(2) \cdot √(17) \cdot √(68)\\&=(1)/(2) \cdot √(17 \cdot 68)\\&=(1)/(2) \cdot √(1156)\\&=(1)/(2) \cdot √(34^2)\\&=(1)/(2) \cdot 34\\&=17 \sf \; units^2\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/6poxm5gztkh4qwz5pldu1jt8mrxouk0jiq.png)
Therefore, the area of the given triangle is 17 units².