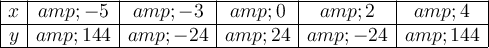Answer:
x-intercepts: -4, -2, 1 and 3
y-intercept: 24
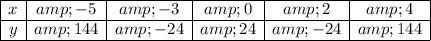
Explanation:
Given polynomial:
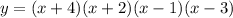
The x-intercepts are the points at which the curve intersects the x-axis, so when the function equals zero.
Zero Product Property
If a ⋅ b = 0 then either a = 0 or b = 0 (or both).
Therefore, to find the x-intercepts, set each factor of the given polynomial equal to zero and solve for x:
Therefore:
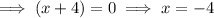

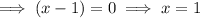
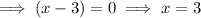
Therefore, the x-intercepts are -4, -2, 1 and 3.
The y-intercept is the point at which the curve intersects the y-axis, so when x is zero.
To find the the y-intercept, substitute x = 0 into the given polynomial:
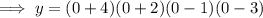
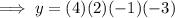
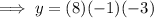
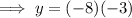
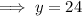
Therefore, the y-intercept is 24.
To find the other points on the graph, substitute each value of x into the polynomial and solve for y:



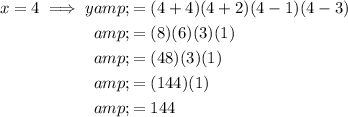
Therefore: