Answer:
x = -1, 7
Explanation:
Given question is incomplete; find the complete question in the attachment.
x² - 6x - 7 = 0
Step 1,
Isolate the constant by ADDING 7 both the sides of the equation.
x² - 6x - 7 + 7 = 0 + 7
x² - 6x = 7
Step 2
Add 9 to both sides of x² - 6x = 7 to form a perfect square trinomial while keeping the equation balanced.
x² - 6x + 9 = 7 + 9
Step 3
Write the trinomial x² - 6x + 9 as (x - 3) squared.
x² - 2(3)x + 9 = 16
(x - 3)² = 4²
Step 4
Use the square root property of the equality to get x - 3 = ± 4
(x - 3)² = 4²
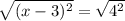
(x - 3) = ±4
Step 5
Isolate the variable to get solution of -1 and 7
x - 3 = ± 4
x = -3 ± 4
x = -1, 7