Answer:
x has no real solutions.
x = 8 + 6i, x = 8 - 6i
Explanation:
First, move the all the terms to one side of the equation.
x^2 - 16x + 100 = -100 + 100
x^2 - 16x + 100 = 0
Then, based on our knowledge of the standard form of a quadratic equation: ax^2 + by + c = 0, we can plug the coefficients in front of the variables into the formula, which looks like
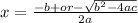 .
.
Our a here is 1,
The b is -16,
The c is 100.
plugging it in:
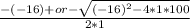
simplifies down to:
16/2 + or - (√(256 - 400))/2
= 8 + or - √(-36)
Here, we have a negative square root, meaning there will be no roots for this equation in the real number system.
If you include imaginary/complex numbers, this equation will have roots.
x = 8 + or - √(-36)
x = 8 + or - 6√(-1)
x = 8 + or - 6i
so the final answer:
x = 8 + 6i, x = 8 - 6i