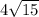Question

What is the shortest possible perimeter for an arrangement with an area of 15 square feet? Please get me the answer as soon as possible!!!!!!!!!!!

Answer 1

The shortest possible perimeter is:
`4√(15)`

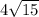
Explanation:

Given

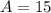`A = 15` --- area

Required

Find the shortest possible perimeter

Area is calculated as:

`A=l * b`

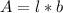
This gives:

`l * b = 15`

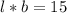
Make l the subject

`l=(15)/(b)`

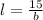
Perimeter is calculated as:

`P =2(l + b)`

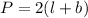
Substitute
`l=(15)/(b)`

`P =2((15)/(b) + b})`

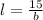
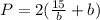
Rewrite as:

`P =2(15b^(-1) + b)`

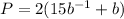
Differentiate and minimize;

`P' =2(-15b^(-2) + 1)`

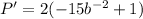
Minimize by equating P' to 0

`2(-15b^(-2) + 1) = 0`

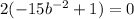
Divide through by 2

`-15b^(-2) + 1 = 0`

`-15b^(-2) = -1`

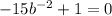
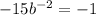
Divide through by -1

`15b^(-2) = 1`

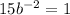
Rewrite as:

`(15)/(b^2) = 1`

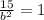
Solve for b^2

`b^2 = (15)/(1)`

`b^2 = 15`

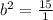
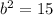
Solve for b

`b = \sqrt{15`

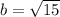
Recall that:
`P =2((15)/(b) + b})`

`P = 2 * ((15)/(√(15)) + √(15))`

`P = 2 * (√(15) + √(15))`

`P = 2 * (2√(15))`

`P = 4√(15)`

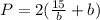
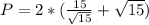
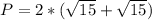
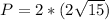
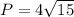
The shortest possible perimeter is:
`4√(15)`