Answer:
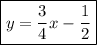
Explanation:
First, we will find the slope. This is done by finding the change in y over the change in x.
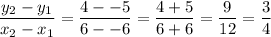
Next, we will find the equation. We will create a point-slope equation and simplify into slope-intercept form.
y - 4 =
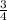 (x - 6)
(x - 6)
y =
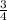 x -
x -
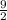 + 4
+ 4
y =
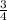 x -
x -
