Answer:
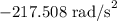
Step-by-step explanation:
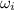 = Initial angular velocity =
= Initial angular velocity =
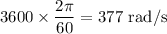
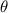 = Angular displacement =
= Angular displacement =

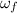 = Final angular velocity = 0
= Final angular velocity = 0
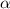 = Angular acceleration
= Angular acceleration
From the kinematic equations of angular motion we have
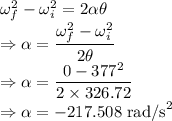
The constant angular acceleration of the centrifuge is
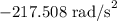 .
.