Question

What translation rule can be used to describe the result of the composition of (x, y) → (x-9, y

-2) and (x, y) + (x + 1, y-2)?
(x, y) = (x+8, y– 4)
(x, y) = (x – 10, y +0)
(x, y) → (x–8. y - 4)
(x, y) = (x - 4. y - 8)

Answer 1

Answer: Choice C

`(x,y) \to (x-8,y-4)`

===================================================

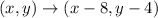
Step-by-step explanation:

The first translation
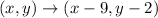`(x,y) \to (x-9,y-2)` has x become x-9. This means we shift 9 units to the left.

The second translation
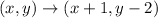`(x,y) \to (x+1,y-2)` tells us to shift 1 unit to the right when going from x to x+1.

Combining the "9 units to the left" and "1 unit to the right" will produce an overall shift of "8 units to the left". It might help to draw out a number line to see this.

After combining those two translations, we'll have
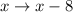`x \to x-8` which means we'll end up with
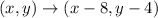`(x,y) \to (x-8,y-4)`. The first two translations shift the point down 2 units at a time, so overall we shift down 4 units.