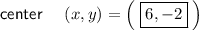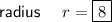Answer:
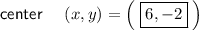
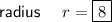
Explanation:

Given equation:
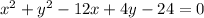
Move the constant to the right side of the equation and collect like variables on the left side of the equation:
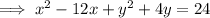
Create perfect square trinomials for the both variables by adding the square of the half the coefficient of x and y to both sides:
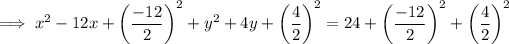
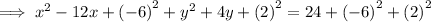
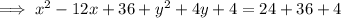
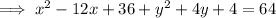
Factor the two perfect trinomials:
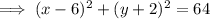
Therefore: