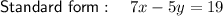Answer:

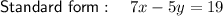
Explanation:
A perpendicular bisector is a line that intersects another line segment at 90°, dividing it into two equal parts.
To find the perpendicular bisector of segment AB, find the slope of AB and the midpoint of AB.
Define the points:
- Let (x₁, y₁) = A(-5, 4)
- Let (x₂, y₂) = B(9, -6)
Slope of AB
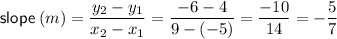
Midpoint of AB
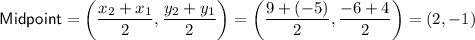
If two lines are perpendicular to each other, their slopes are negative reciprocals.
Therefore, the slope of the line that is perpendicular to line segment AB is ⁷/₅.
Substitute the found perpendicular slope and the midpoint of AB into the point-slope formula to create an equation for the line that is the perpendicular bisector of line segment AB:
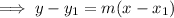
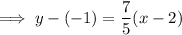
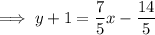
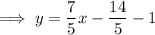
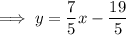
Therefore, the formula that expresses the fact that an arbitrary point P(x, y) is on the perpendicular bisector of segment AB is: