Answer:
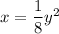
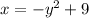
Explanation:
Functions are symmetric with respect to the x-axis if for every point (a, b) on the graph, there is also a point (a, −b) on the graph:
To determine if a graph is symmetric with respect to the x-axis, replace all the y's with (−y). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the x-axis.
Therefore, any function that includes the term y² will be symmetric with respect to the x-axis since (-y)² = y².
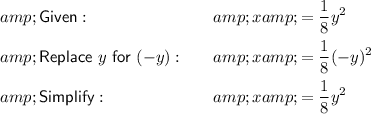
Therefore, since the resultant expression is equivalent to the original expression, it is symmetric with respect to the x-axis.

Therefore, since the resultant expression is equivalent to the original expression, it is symmetric with respect to the x-axis.