Answer: The equation defines the relationship between the angle of inclination of the line relative to the x-axis and the point at which the line passes through the y-axis on a graph.
Explanation:
Imagine a line, L, that passes through the y-axis of a graph at some point B=(0,b), where the 0 is the x-coordinate of B and b is the y-coordinate of B. In this case, we will use the variable m to represent the slope of the line. Geometrically, the slope of a line is said to be tangent to its angle of inclination, the smaller of the two angles formed by the line L and the x-axis. In trigonometry, the tangent of an angle in a right triangle is defined as the ratio of the side opposite of it over the side adjacent to it. This relationship can be illustrated by constructing a right triangle where the hypotenuse is formed by the segment of the line L between the point B and an arbitrary point P somewhere along the line with the coordinates (x,y).
This triangle can be seen in the attached jpg. The side opposite of the angle of inclination is the imaginary vertical line formed between the point P and the x axis and the side adjacent to it is formed by the imaginary horizontal line between the point B and the vertical line from P. The point where these imaginary lines intersect forms the right angle of the triangle. The length of the opposite side, l1, can be expressed as the difference in y between points P and B:
l1 = y-b
Likewise, the length of the adjacent side, l2, can be expressed as the difference in x between points P and B:
l2 = x-0
The tangent of the angle of inclination, labled as
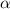in the picture, can then be expressed as:
tan(
) =
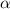simplified as:
tan(
) =
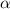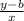
Because we know that slope m = tan(
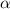), we can say that
m =
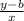
solving by algebra for y,
mx + b = y or y = mx + b
in single variable calculus, the slope of a line is described as the rate of change of its y coordinates with respect to the rate of change of its x coordinates, referred to as the derivative of y with respect to x. This relationship is used to describe things like the speed of an object as it relates to the change in the objects position. The important thing to realize here is the connection between the slope, which we expressed as the difference in the y values of two points on a line over the difference in their x values, and the behavior of the coordinates of points as you move along the line.
Hope that helps! If the last bit is confusing, don't worry, as long as you understand why y=mx+b is the slope intercept form you've got the right idea.